Impossible problems | The game of science

The typical lamp that is turned on and off from two switches (one of which frequently fails, causing an uncomfortable going back and forth from one switch to another until the light is turned on), mentioned last week, works according to the scheme of the figure.

When both switches make contact at A, or both at B, the circuit is closed and the lamp lights; otherwise, the circuit is cut off and the lamp goes out. (In the diagram everything seems very simple; it is another thing to connect the cables properly in a real installation).

Our regular commentator Luca Tanganelli takes the question a step further and asks what the circuit would be like if the same lamp were turned on and off from three switches. What if we generalize the problem to a lamp with n switches?

As for the unknown switch bulb, this is Vicente Pardo’s solution:

“You flip the first switch and wait (let’s say three minutes), you turn it off and you flip the next one and you run upstairs. Three possibilities: the light bulb is on, which confirms the second switch you just flipped; if the light bulb is off you go over and touch it with your hand, if it is hot it is the first switch you operated for three minutes and if it is cold it is the third switch ”.

A word of advice: if you wait three minutes, don’t run upstairs or, if the good one was the first switch, you would burn your hand.

Back to geometry

After a few weeks wandering around physics and its surroundings, and before the purists who insist that this is a math section get upset, let’s get back to geometry with a couple of seemingly impossible problems, one for lack of data and the other by excess.

The first appeared in Martin Gardner’s wonderful recreational mathematics section in American scientist:

Divide an obtuse triangle into acute triangles or show that it is impossible.

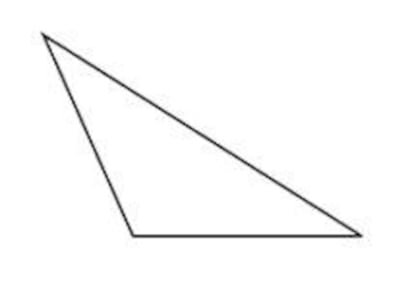
The second I saw in one of Clifford Pickover’s highly recommended books (I can’t remember which one; maybe some reader knows) and although in its original version it had to do with a spherical spaceship and an alien with tentacles, in short, it says So:

The area of ​​a sphere and its volume are both four-digit whole numbers multiplied by π. What is the radius of the sphere?

And since we have a sphere at hand, let’s imagine that it is filled with a gas whose molecules are stirring inside. Will there be a plane at all times that cuts the sphere so that there are the same number of molecules on each side of it? (The number of molecules inside the sphere is supposed to be even, of course).

By the way, this installment of The game of science published on 12 11 21. What can my astute readers say about the elegant palindrome 121121?

Carlo Frabetti is a writer and mathematician, member of the New York Academy of Sciences. He has published more than 50 popular science works for adults, children and young people, including ‘Damn physics’, ‘Damn maths’ or ‘The great game’. He was a screenwriter for ‘La bola de cristal’.

You can follow MATTER on Facebook, Twitter me Instagram, or sign up here to receive our weekly newsletter.